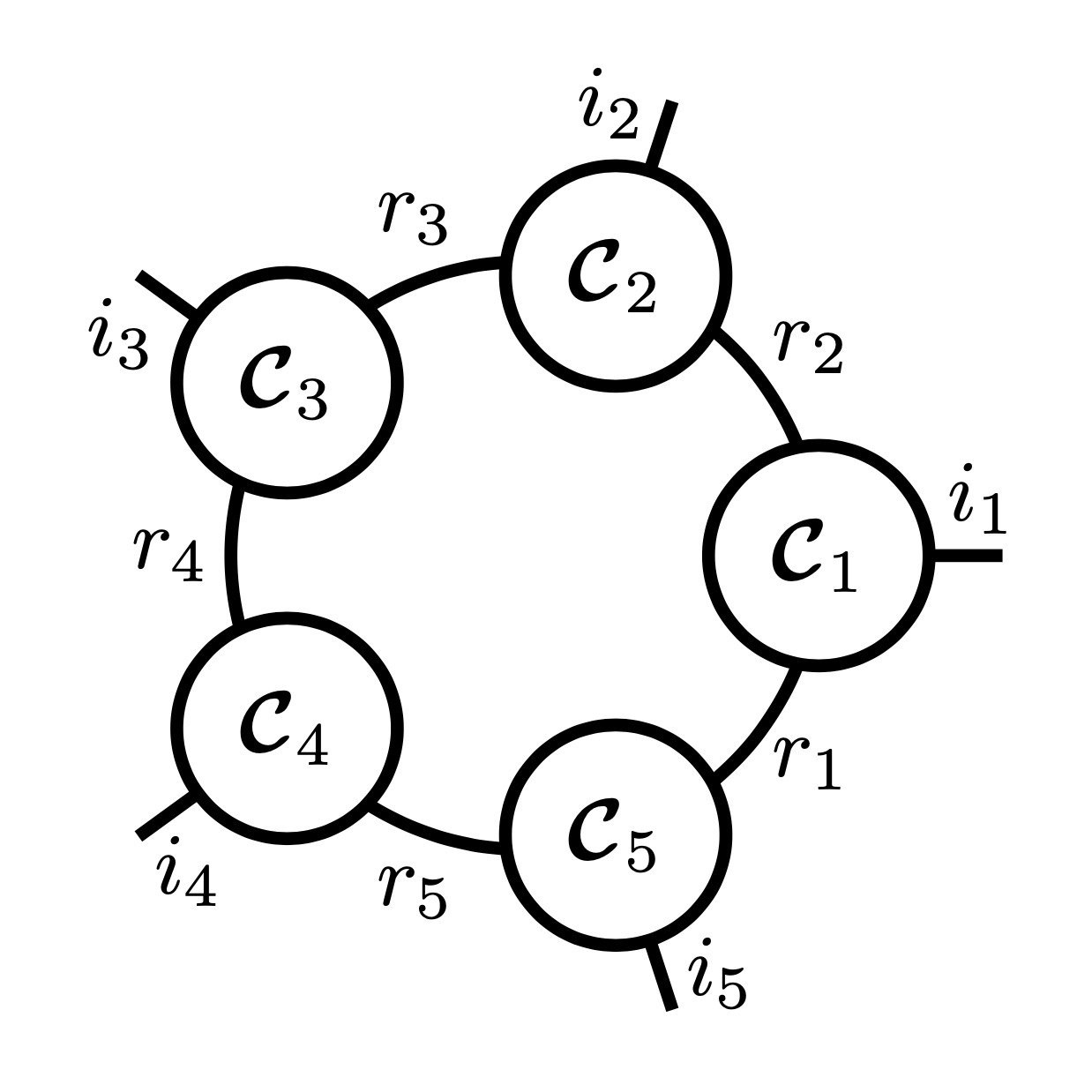
Abstract
We introduce T-Basis, a novel concept for a compact representation of a set of tensors, each of an
arbitrary shape, which is often seen in Neural Networks. Each of the tensors in the set is modeled
using Tensor Rings, though the concept applies to other Tensor Networks. Owing its name to the T-shape
of nodes in diagram notation of Tensor Rings, T-Basis is simply a list of equally shaped
three-dimensional tensors, used to represent Tensor Ring nodes. Such representation allows us to
parameterize the tensor set with a small number of parameters (coefficients of the T-Basis tensors),
scaling logarithmically with each tensor's size in the set and linearly with the dimensionality of
T-Basis. We evaluate the proposed approach on the task of neural network compression and demonstrate
that it reaches high compression rates at acceptable performance drops. Finally, we analyze memory and
operation requirements of the compressed networks and conclude that T-Basis networks are equally well
suited for training and inference in resource-constrained environments and usage on the edge devices.
Paper
Check out the full paper on arXivPatent
One patent "Method and system for compressing a neural network" pendingSource code
T-Basis
: The official repository of this project
Subscribe to my Twitter feed to receive updates about this and my other research!
ICML'2020 Video Poster
Citation
@InProceedings{obukhov2020tbasis,
title={T-Basis: a Compact Representation for Neural Networks},
author={Obukhov, Anton and Rakhuba, Maxim and Georgoulis, Stamatios and Kanakis, Menelaos and Dai, Dengxin and Van Gool, Luc},
booktitle={Proceedings of the 37th International Conference on Machine Learning},
pages={7392--7404},
year={2020},
editor={Hal Daumé III and Aarti Singh},
volume={119},
series={Proceedings of Machine Learning Research},
month={13--18 Jul},
publisher={PMLR},
pdf={http://proceedings.mlr.press/v119/obukhov20a/obukhov20a.pdf},
url={http://proceedings.mlr.press/v119/obukhov20a.html}
}