Abstract
We study low-rank parameterizations of weight matrices with embedded spectral properties in the Deep
Learning context. The low-rank property leads to parameter efficiency and permits taking computational
shortcuts when computing mappings. Spectral properties are often subject to constraints in optimization
problems, leading to better models and stability of optimization. We start by looking at the compact
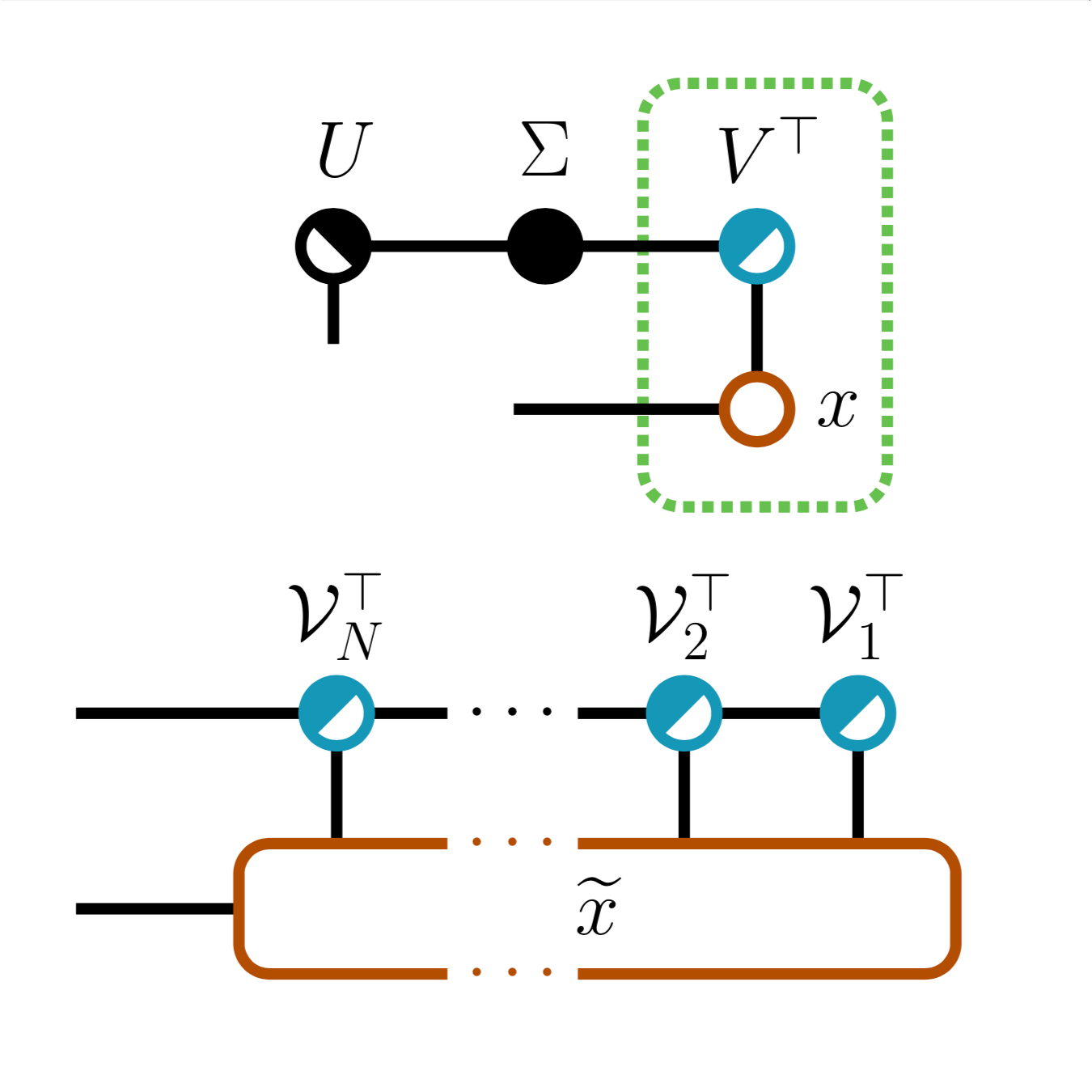
SVD parameterization of weight matrices and identifying redundancy sources in the parameterization. We
further apply the Tensor Train (TT) decomposition to the compact SVD components, and propose a
non-redundant differentiable parameterization of fixed TT-rank tensor manifolds, termed the Spectral
Tensor Train Parameterization (STTP). We demonstrate the effects of neural network compression in the
image classification setting and both compression and improved training stability in the generative
adversarial training setting.
Paper
Check out the full paper on arXivPoster
View the conference posterPatents
Two patents pending, both titled "Efficient and stable training of a neural network in compressed form": 1 , 2Source code
STTP
: The official repository of this project
Subscribe to my Twitter feed to receive updates about this and my other research! Also, check out the following projects related to this work:
-
torch-householder: Efficient Householder Transformation in PyTorch -
torch-fidelity: High-fidelity performance metrics for generative models in PyTorch
Presentations
- AISTATS 2021
- Sparsity in Neural Networks 2021 Workshop
- ICVSS 2022
AISTATS'2021 Teaser Video
Citation
@InProceedings{obukhov2021spectral,
title={Spectral Tensor Train Parameterization of Deep Learning Layers},
author={Obukhov, Anton and Rakhuba, Maxim and Liniger, Alexander and Huang, Zhiwu and Georgoulis, Stamatios and Dai, Dengxin and Van Gool, Luc},
booktitle={Proceedings of The 24th International Conference on Artificial Intelligence and Statistics},
pages={3547--3555},
year={2021},
editor={Banerjee, Arindam and Fukumizu, Kenji},
volume={130},
series={Proceedings of Machine Learning Research},
month={13--15 Apr},
publisher={PMLR},
pdf={http://proceedings.mlr.press/v130/obukhov21a/obukhov21a.pdf},
url={http://proceedings.mlr.press/v130/obukhov21a.html}
}